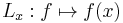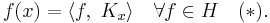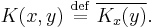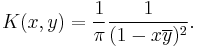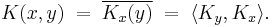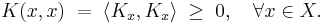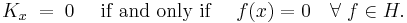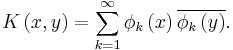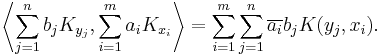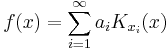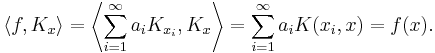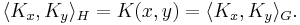Reproducing kernel Hilbert space
In functional analysis (a branch of mathematics), a reproducing kernel Hilbert space is a Hilbert space of functions in which pointwise evaluation is a continuous linear functional. Equivalently, they are spaces that can be defined by reproducing kernels. The subject was originally and simultaneously developed by Nachman Aronszajn (1907–1980) and Stefan Bergman (1895–1977) in 1950.
In this article we assume that Hilbert spaces are complex. The main reason for this is that many of the examples of reproducing kernel Hilbert spaces are spaces of analytic functions, although some real Hilbert spaces also have reproducing kernels.
An important subset of the reproducing kernel Hilbert spaces are the reproducing kernel Hilbert spaces associated to a continuous kernel. These spaces have wide applications, including complex analysis, quantum mechanics, statistics and harmonic analysis.
Contents |
Definition
Let X be an arbitrary set and H a Hilbert space of complex-valued functions on X. We say that H is a reproducing kernel Hilbert space if every linear map of the form
from H to the complex numbers is continuous for any x in X. By the Riesz representation theorem, this implies that for every x in X there exists a unique element Kx of H with the property that:
The function Kx is called the point-evaluation functional at the point x.
Since H is a space of functions, the element Kx is itself a function and can therefore be evaluated at every point. We define the function 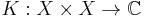 by
by
This function is called the reproducing kernel for the Hilbert space H and it is determined entirely by H because the Riesz representation theorem guarantees, for every x in X, that the element Kx satisfying (*) is unique.
Examples
For example, when X is finite and H consists of all complex-valued functions on X, then an element of H can be represented as an array of complex numbers. If the usual inner product is used, then Kx is the function whose value is 1 at x and 0 everywhere else, and K(x,y) can be thought of as an identity matrix since K(x,y)=1 when x=y and K(x,y)=0 otherwise. In this case, H is isomorphic to 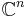 .
.
A more sophisticated example is the Hardy space H2(D), the space of square-integrable holomorphic functions on the unit disc. So here X=D, the unit disc. It can be shown that the reproducing kernel for H2(D) is
This kernel is an example of a Bergman kernel, named for Stefan Bergman.
Properties
The reproducing property
It is clear from the discussion above that
In particular,
Note that
Orthonormal sequences
If 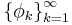 is an orthonormal sequence such that the closure of its span is equal to
is an orthonormal sequence such that the closure of its span is equal to  , then
, then
Moore-Aronszajn theorem
In the previous section, we defined a kernel function in terms of a reproducing kernel Hilbert space. It follows from the definition of an inner product that the kernel we defined is symmetric and positive definite. The Moore-Aronszajn theorem goes in the other direction; it says that every symmetric, positive definite kernel defines a unique reproducing kernel Hilbert space. The theorem first appeared in Aronszajn's Theory of Reproducing Kernels, although he attributes it to E. H. Moore.
Theorem. Suppose K is a symmetric, positive definite kernel on a set E. Then there is a unique Hilbert space of functions on E for which K is a reproducing kernel.
Proof. Define, for all x in E, 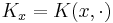 . Let H0 be the linear span of
. Let H0 be the linear span of 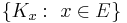 . Define an inner product on H0 by
. Define an inner product on H0 by
The symmetry of this inner product follows from the symmetry of K and the non-degeneracy follows from the fact that K is positive definite.
Let H be the completion of H0 with respect to this inner product. Then H consists of functions of the form
where 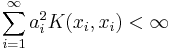 . The fact that the above sum converges for every x follows from the Cauchy-Schwarz inequality.
. The fact that the above sum converges for every x follows from the Cauchy-Schwarz inequality.
Now we can check the RKHS property, (*):
To prove uniqueness, let G be another Hilbert space of functions for which K is a reproducing kernel. For any x and y in E, (*) implies that
By linearity,  on the span of
on the span of 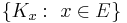 . Then G = H by the uniqueness of the completion.
. Then G = H by the uniqueness of the completion.
Bergman kernel
The Bergman kernel is defined for open sets D in Cn. Take the Hilbert H space of square-integrable functions, for the Lebesgue measure on D, that are holomorphic functions. The theory is non-trivial in such cases as there are such functions, which are not identically zero. Then H is a reproducing kernel space, with kernel function the Bergman kernel; this example, with n = 1, was introduced by Bergman in 1922.
See also
Notes
References
- Aronszajn, Nachman (1950). "Theory of Reproducing Kernels". Transactions of the American Mathematical Society 68 (3): 337–404. doi:10.1090/S0002-9947-1950-0051437-7. JSTOR 1990404. MR51437.
- Alain Berlinet and Christine Thomas, Reproducing kernel Hilbert spaces in Probability and Statistics, Kluwer Academic Publishers, 2004.
- Kimeldorf, George; Wahba, Grace (1971). "Some results on Tchebycheffian Spline Functions". Journal of Mathematical Analysis and Applications 33 (1): 82–95. doi:10.1016/0022-247X(71)90184-3. MR290013. http://www.stat.wisc.edu/~wahba/ftp1/oldie/kw71.pdf.
- Grace Wahba, Spline Models for Observational Data, SIAM, 1990.
- Cucker, Felipe; Smale, Steve (2002). "On the Mathematical Foundations of Learning". Bulletin of the American Mathematical Society 39 (1): 1–49. doi:10.1090/S0273-0979-01-00923-5. MR1864085.